The Thiele-Small Parameters for Measuring, Specifying and Designing Loudspeakers

- Neville Thiele

Introduction.

The loudspeaker parameters were first described by Thiele in 1961[1], but were not accepted widely until after they were republished in the Journal of the Audio Engineering Society in 1971, and Small, over the next three years, published a series of papers [2-8] that expanded them and made them much more understandable and useful. Over the last thirty years, they have been used widely, almost universally, to characterise loudspeaker drivers and thus facilitate the design of loudspeaker systems. However, some aspects of their measurement procedure and their use have attracted a degree of misunderstanding. The paper will try to correct these misunderstandings and put some aspects of the measurements into a better perspective.

Limitations .

First of all, it is often emphasised that the parameters provide only an approximate understanding to the performance of a loudspeaker. It must be understood that the approximation, with these parameters, is sufficiently close as to predict performance within a dB or so. Nevertheless it is an approximation. Any engineering theory is, after all, a simplification of what happens in the “real world”, and to that extent an approximation. For this reason “theoretical predictions” sometimes fail, to the great glee of those who do not fully understand them, not from failure of the basic theory but more usually through its application to circumstances where its ideal, simplifying, assumptions no longer hold.

We consider now some of the assumptions inherent in applying the parameters. First, it is assumed that the driver’s efficiency is negligibly small. Some drivers with light cones and large magnets that produce a high flux can provide efficiencies as high as 4%, i.e. they produce acoustic output power 14 dB lower than the electrical input power. Since one acoustic watt radiated isotropically into half space, i.e. on one side of a flat baffle, produces a sound pressure level relative to reference level (SPL) of +112 dB at 1 metre, a loss of 14 dB corresponds to an SPL of +98 dB. But small as that may be, the majority of drivers are even less efficient. Drivers have become less efficient generally since the 1961 paper as transistor amplifiers with higher electrical output power (e.g. 150 watts, compared with the 15 watts that was considered large from a valve amplifier) have become available at a reasonable expense and made it practical for drivers to use heavier cones and overhung voice coils in the quest for lower distortion. Nowadays a driver that produces an SPL of +85dB at 1 metre from a 1 watt input. i.e 1s 0.2% efficient, is not at all unusual.

Second, because a loudspeaker driver presents an impedance that varies widely with frequency, it has become conventional to express its sensitivity in terms of its Power Available Efficiency (PAE), i.e. the ratio of its acoustic power output to the “available” electrical power input that it would have absorbed if it had presented to the input a pure resistance equal to its d.c. resistance R_E .

Third, the parameters apply only over the “piston range” of frequencies where driver acts as a true piston, i.e. at the lower frequencies where the wave number ka is less than 1.

where w = 2πf

f is the operating frequency

r is the radius of the piston, and

c is the velocity of sound

Taking c, the velocity of sound, as 344 m/s or 1130 ft per sec then ka is 1 at 4300 Hz for a piston of 1 inch diameter, i.e. ½ inch radius, or at 360 Hz for a piston of 12 inch diameter, and the parameters apply at frequencies lower than these limits.

This shows that the frequency range over which these “low frequency” parameters apply varies with the radius, or diameter, of the cone, so they are equally useful in assessing the performance of tweeters as of woofers. Beranek [9] incidentally places the limit of the piston range an octave lower, where ka = ½, where the frequency response has deviated from the ideal by 0.2 dB. At ka = 1, however, the error is still only 0.7 dB. At frequencies above this the power radiated by a piston falls towards an ultimate slope of 6dB per octave. However the pressure response of a piston also tends to focus into an increasingly narrow beam as the frequency rises so that with skilful design, a driver can radiate a comparatively constant, ”flat”, pressure response at much high frequencies to a listener on its axis even though the total power that it radiates into the whole space, is falling.

Fourth, the parameters characterise only the “small signal” performance of a loudspeaker. As the signal level increases, a driver becomes more and more non-linear, and much of the skill in designing a driver goes into making it perform linearly to a high level. A number of researchers, particularly Klippel [10], have shown how the different sources of non-linearity, in the effective flux through the voice coil, in the compliance of the restraint by the edge surround and the spider, in the effective inductance of the voice coil, and even to a smaller extent in frequency modulation of higher frequencies by lower frequencies due to the Doppler effect, can be separated and hence dealt with separately in the design.

However, because much of the programme signals that a loudspeaker handles are at the lower levels, and because a good loudspeaker can handle these signals linearly to sufficiently high levels, these parameters remain among the most important tools in specifying loudspeaker performance and, for forty years, have stood the test of time.

The Parameters

Four main parameters characterise the performance of a loudspeaker driver and are used to calculate its performance when it is mounted in an enclosure or box.

f_S the resonance frequency of the driver in Hz

Q_E the ‘electrical’ quality factor, the ratio of the d.c. resistance of the voice coil to reactance at resonance of the drivers motional impedance. It is a pure, dimensionless, number

Q_M the ‘mechanical’ quality factor, the ratio of the shunt resistance of the driver’s motional impedance to its reactance at resonance, another pure number. In some early publications, Thiele has called this parameter Q_A for ‘acoustical’.

The Q values, quality factors, affect the damping of the driver around its resonance. The higher the Q’s the more the frequency response at resonance will peak compared with the in-band response at higher frequencies. If the Q’s are too low the frequency response will sag around resonance. In applications where the input impedance affects the response, as in passive crossover networks, Q_E and Q_M affect the input impedance of the driver in different ways and are therefore significant separately.

However when, as is more usual, the driver is fed from an amplifier whose output that presents a low impedance, the two Q’s act together to control damping near resonance, and it is convenient to combine them into Q_T , the “total” quality factor

in the manner of resistances in parallel, which is of course, how they act.

When these parameters f_S Q_M Q_E and Q_T are measured under different conditions and their values change somewhat, i8t is convenient to characterise each of them with a second sub-script. Thus

f_SA is the value of f_S that is measured when the driver is unbaffled, hanging “in air”.

f_SB, slightly lower, is the value of f_S when the driver is mounted on an effective baffle, i.e. in any box,

f_SC is the resonance frequency of the system of a driver mounted in a closed box.

Similarly Q_MA Q_MB Q_MC, Q_EA Q_EB Q_EC and Q_TA Q_TB Q_TC.

V_AS, the volume of air equivalent to the acoustical compliance of the driver. It may be specified in litres (i.e. cubic decimetres or milli-cubic-metres) or in Imperial units of cubic feet or cubic inches. This parameter V_AS affects the response through its ratio with V_B , the volume of the box that the driver is mounted in. That ratio may be written as V_AS/V_B , but more often as the ratio of the two compliances C_AS/C_AB . The user must be warned that because the volume (compliance) of the box forms the denominator of the expression, the bigger the box the smaller is the figure for C_AS/C_AB . In his publications, Small has called this quantity α.

These four parameters of the driver (or three once Q_E and Q_M are combined into Q_T) , along with V_B , the volume of the box, control the smoothness of response that is obtained from a loudspeaker driver/box combination and to them must be added, whenever the box is vented (ported), the box resonance f_B , the frequency where the mass of the vent resonates with the compliance of the air in the box. It is most easily visualised (!), for example, as the frequency of the note that results from blowing across the top of a bottle, which is of course can be considered as another variant of the Helmholz resonator.

Two other parameters are of lesser, but still significant, importance in some designs. One Q_L , the “leakage” Q, has a small effect in vented box designs. The other, L_E , the voice coil inductance in series with R_E ,must be treated with care. It is not invariant, as would usually be expected from an inductance, but varies inversely with the square root of frequency. These two parameters will be discussed in detail later.

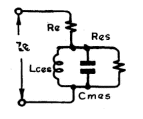
The driver is specified in terms of the electrical impedance diagram of Fig. 1. In this, R_E is the d.c resistance of the driver. The rest of the network, consisting of the three elements C_MES L_CES and R_ES in parallel, is the “motional impedance” of the driver. It is produced by the interaction of the motion of the cone, through the voice coil, with the flux of the magnet. If the motion is blocked, this motional impedance falls to zero.

We specify the driver in terms of the network of Fig. 1 with the four parameters, R_E f_S Q_M and Q_E .

and

where

f_S being the resonance frequency of the driver. We also need to determine V_AS , the volume of air equivalent to the acoustical compliance of the driver.

The Transfer Functions of Loudspeakers

In the next section, we show how the performance of a loudspeaker system may be found using these parameters. In this paper we do not derive the expressions using the electrical equivalents of the acoustical properties of the system. That is found in other papers. We present here the results of those derivations, the transfer functions that, applied to the reader’s own calculations, or better and more easily still a computer program, can be taken as a recipe for finding the responses. A set, or constellation, of parameters needed to produce a given result is often called an ‘alignment’.

The transfer function relating the acoustical output pressure to the electrical input voltage is written most compactly in the “operational” form of the Laplace transform, from which the amplitude, phase and transient responses can be calculated.

Closed Box.

The transfer function of the loudspeaker in a totally enclosed box is, in the operational form,

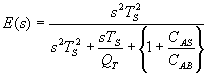
where

and f_S is the resonance frequency of the driver. In early papers, written before 1965 approximately, “s” is written as “p”. The meaning is the same, only the convention has changed. Also C_AS/C_AB, the compliance ratio of the driver to the box is written more appropriately for calculation as V_AS/V_B, the ratio of the effective acoustic volume of the driver to the volume of the box. Q_T , as described earlier, is the “total” Q (quality or loss) factor of the box, obtained by combining the “mechanical” Q_M with the “electrical” Q_E .

We can write the expression in the “jw” form from which the amplitude and phase responses can be calculated more easily. We simply replace “s” with “jw” and remember that ( j )² = -1, ( j )³ = -j, ( j )⁴ = 1 etc. and that w = 2pf, where f is the frequency being considered

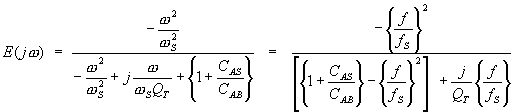
To calculate the squared magnitude of that expression we square the sum of the “real” components (those not multiplied by j) and square the sum of the “imaginary” components (those that are multiplied by j) and add the squares together. Then 10 times the logarithm of that squared magnitude is the response in dB. Thus

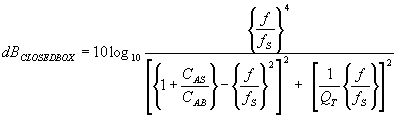
The expression shows that, for a driver mounted in an enclosed box, the lowest cut-off frequency is

f_SÖ(1 + C_AS/C_AB). Thus it can never be lower than f_S , and then only when C_AS/C_AB is zero, i.e. when the box is infinitely large. When C_AS/C_AB is 1, the cut-off frequency is 1.414 f_S; when C_AS/C_AB is 3, it is 2 f_S.

Vented Box.

The transfer function of the loudspeaker in the vented box is, in the operational form,

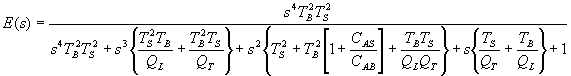
where Q_L is the “leakage Q”, considered as a parameter of the driver. In the 1961 paper, Thiele calculated a similar parameter Q_B, the “box Q”, as a parameter of the box. When Small showed later that such leakage losses were much greater in the driver than those in the box, so much so that they could be virtually ignored, he still called the changed parameter Q_B initially, but later called it Q_L. Thus in the expression above, Q_L is the loss parameter for the driver, as calculated below. If Q_L is not known, it may be taken as 7 without too much error. If on the other hand Q_L is ignored, as in some of the earlier papers, it is effectively taken as infinite and all the terms containing it disappear in the expression above.

Also

where f_B is the resonance frequency of the box.

The expression becomes, in the jw form,

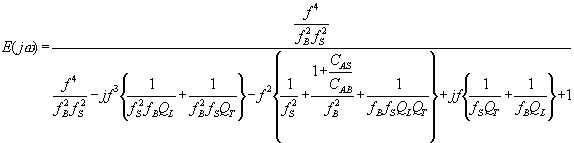
from which the response is calculated, first as the squared magnitude and then as decibels,

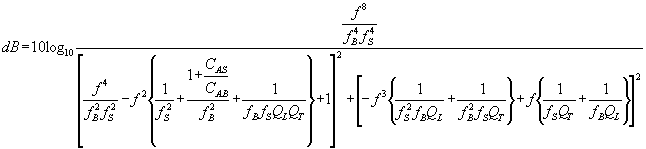
When the vent is closed up, then f_B diminishes towards zero, and only the terms that contain f_B² contribute significantly to the denominator of the expression above. If then the insignificant terms are removed and the remaining terms multiplied by (f_B/f)² and, remembering that the denominator terms are later squared, the numerator is multiplied complementarily by (f_B/f)⁴, the dB response becomes, not surprisingly, the same as for the closed box. Thus the same calculation as for the vented box can be used for the closed box, so long as a box resonance figure much lower than f_S, e.g. 1 Hz, is entered for f_B.

Fig 4 shows that, with a vented box system, unlike a closed box, the response cam be extended half an octave below the driver resonance f_S, if the box is larger (C_AS/C_AB smaller), its tuning frequency f_B is lower than f_S and Q_T is comparatively high. The response could be extended even lower but the response ripple, that can be seen already in curve no 8, would increase excessively. When the box is small (C_AS/C_AB greater than 2) f_B tuned higher than f_S and Q_T comparatively low, a response free of peaks can be realised, but its cut-off frequency f₃ rises rather higher.

The compliance of a driver may increase with time, particularly after it has been “exercised” by use. When this happens, both f_S and the Q’s will decrease in inverse proportion to the square root of the compliance. In a vented box system, this has surprisingly little effect on the response, so long as it is the only parameter that has changed.

Equalization. *

Once the transfer function of a loudspeaker has been found, as above, it can be used to equalize an undesirable alignment to a desirable one [11, 12]. The second order transfer function of a closed box loudspeaker, or the two second order factors of the fourth order transfer function of a vented box loudspeaker are taken as the numerator(s) of biquadratic active filter(s) whose denominator(s) realise the desirable transfer function(s)

*This section is extracted from ref.12

In this way, any loudspeaker transfer function can, in principle, be equalized to any desired function. We say “in principle” as a reminder of the practical limitations. The parameters of the loudspeaker or the equalizer may change with production tolerances or age. It is therefore important not to try to equalize too high or narrow a response peak with a complementary notch, otherwise a small drift in the responses of loudspeaker or equalizer may make the equalized result worse than it was in the first place. Similarly, an equalizer that restores a falling loudspeaker response too enthusiastically may well demand excessive power from the amplifier at some frequencies and make it distort at unexpectedly low levels of output signal.

Again, it is important to remember that, in a vented system, the acoustic output of the vent assists the acoustic output from the cone at frequencies above the box resonance, but works against it at frequencies below. At these lower frequencies the cone must execute larger and larger excursions to produce smaller and smaller acoustic outputs. The box resonance should therefore always be placed at the bottom useful limit of the desired equalized response.

In loudspeakers with both vented and sealed enclosures, the excursion of the voice coil rises to a maximum at lower frequencies where they no longer radiate useful acoustic power, as shown in Fig 5. All its excursions result from Butterworth responses, which are 3 dB down when f/ f_B = 1 and fall rapidly at frequencies below. It is therefore beneficial to both the driver and its associated amplifier to provide additional high-pass filtering in that region.

Fig 5 shows how the addition of further second order filtering, that takes the transfer function of a loudspeaker with a closed box from 2^nd order to 4^th order Butterworth (dashed curves 2¢, 3¢ & 4¢) or with a vented box from 4^th order to 6^th order Butterworth (solid curves 4, 5 & 6), provides protection against excessive excursion [11]. Two extra orders are the maximum needed. A brick-wall filter, even were it feasible, would provide little extra effective protection.

Fig 5 shows in fact that even first order auxiliary filtering, which takes the transfer function of a closed box to 3^rd order or a vented box to 5^th order, affords very worthwhile protection. It can be provided with the utmost simplicity, by suitable proportioning of a CR coupling network and adjustment of the associated transfer function(s), to ensure the desired, usually maximally flat, overall response.

Increasing the order of filtering in any system increases the group delay error at the band edge, and is often deprecated for that reason. However the increase in group delay error occurs very much in the last half-octave before cut-off. Further when the cut-off frequency of a high-pass system is lowered, e.g. by equalization, its group delay error at higher frequencies is actually diminished [13].

Measurement of the Parameters.

The parameters of a driver will often be published by the manufacturer, but if they are not or if there is any doubt, e.g. due to spread of values during manufacture or a suspicion of optimism in the manufacturer’s specification, the designer may wish to measure them himself. They may be measured in a number of different ways, for which various advantages are claimed. However the writer believes that the original method given in Fig. 3 from ref. 1, is still as satisfactory as or better than any, so long as the readings are taken with proper care and using the modifications to the procedures described below.

Measurement “In Air”

First of all the driver is measured in air, preferably at least 50 cm from reflecting surfaces. The equipment required is simple. It comprises --

(i) an oscillator, a source of sine wave signals of known frequency. If a frequency counter is not provided integral with the oscillator a separate frequency counter is required. The oscillator should be capable of producing signals up to 10 times below and 20 times above the resonance frequency of the driver. Thus for a driver with a resonance of 50 Hz, the oscillator should cover a range from 5 Hz to 1000 Hz

(ii) a voltmeter and

(iii) an ammeter, both accurate across the range of frequencies used in the tests

(iv) a testing box of known volume in which the driver may be mounted. Preferably, it should be vented and resonant at a frequency near that of the driver, though neither is absolutely necessary. It should not contain acoustically absorbent material.

The first time three instruments provide electrical measurements. The fourth, the testing box, is the only “acoustic” parameter needed in the measurements.

The oscillator must be capable of being read to a precision rather better than 1 Hz, preferably

0.1 Hz. For this reason a frequency counter is a most desirable accessory. If the counter can read frequency only, a measurement with a precision of 0.1 Hz requires a gate period of 10 seconds for each measurement. But if the counter reads “time”, the period of one cycle can be measured and its reciprocal taken as the frequency. When, as is usual, the period of one cycle is measured to a resolution of 0.1 ms, the frequency of a 50 Hz signal can be read to within 1 part in 200,000. Some of the better oscillators measure the period at low frequencies and then convert it internally into a display of frequency

It will be seen that, in the calculations below, two steps depend on the differences between two frequencies and that if these frequencies are, for example, 30 Hz apart, even a precision of 0.1 Hz in their difference only ensures an accuracy in that calculation of 1 in 300, i.e. 0.3%. For this reason care in observation and precision of instrumentation is needed at all times in the measurement of frequency.

The absolute calibration of the ammeter is not important, but its reading must be linear across its whole scale and it must maintain that linearity over the whole range of frequencies being measured so as to ensure accuracy of the ratios of its measurements.

In an alternative method, the ammeter is replaced by a variable resistance that is adjusted for each reading so as to keep the voltmeter reading constant and is then measured to a good precision after each reading, e.g. by a digital ohmmeter.

The voltmeter is needed simply to maintain a constant voltage during the measurement and to draw a current that is very much smaller than that drawn by the device under test. Its indication must also remain constant with frequency. An oscilloscope can perform this function excellently.

The box needs to be free of leaks - a colleague once suggested that it should be specified as not so much airtight as watertight - and to have an opening that seals well to the driver during the reading. It must be rigid and free of internal damping material.

Measurements of frequencies at peaks of impedance can be made more easily and accurately by searching for zero phase angle between the voltage from the oscillator and that across the driver, using the x-y facility of an oscilloscope. The sensitivity of such a reading that incorporates phase measurement can be seen in Fig 6, where the frequencies of the maxima and minima of impedance are measured much more sensitively as the zero crossings of the plot of phase angle. Fig 7 shows that, even when the phase difference between the X and Y deflection voltages is as small as 1°, a (highly squeezed) ellipse can still be seen.

The reading of R_E is taken preferably at d.c. with the oscillator replaced by a battery, but alternatively at a frequency very much, say 10 times, lower than the driver resonance. The next reading is taken at the driver resonance frequency f_S and its resistance R_ES, which the writer now prefers to call R₀ , noted. When an ammeter is used, the reciprocal of the current reading (1 / I) is noted, as if it was the resistance with a notional 1 volt signal.

Then two frequencies are found either side of resonance where the resistance or current has the same intermediate value, R₁ or I₁ , and their two values f₁ and f₂ noted. Unfortunately, in Fig 2 which is reproduced from Fig 16 of ref. 1, R₁ was drawn rather high up the bell-shaped curve, which has led a number of readers to imagine than it is intended to be at 0.707 times the peak impedance, the so-called

“-3dB point” where readings of Q such as this are taken conventionally in radio frequency measurements. Even Fig 8 could give a misleading impression unless we assume that the scale for its Y impedance axis is logarithmic.

However the “-3 dB” method is suitable only for measurement of Q‘s greater than 5. The method proposed below measures Q’s of any value. It will be seen that an accurate calculation of Q_M , and hence of Q_E and Q_T , depends critically on an accurate measurement of the frequency difference f₂ - f₁ , which are taken for the same value of r₁. This requires both accurate readings of f₁ and f₂ and a testing procedure in which the two frequencies are separated as far as possible.

The optimum value of R₁ or I₁ for taking these frequencies is at the geometric mean between their readings at d.c and at resonance, in other words when either

or

Such a reading not only produces good separation between f₁ and f₂. It is also the point on the curve of Z_E vs. frequency in Fig. 2 where the slope is a maximum and thus the frequencies can be read most sensitively.

These are all the “In Air” readings that are required. but it is worthwhile to check also for consistency that

Now the ratios are calculated

or

or

and then the parameters

: :

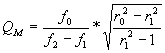
It should be noted that

i.e. Q_E and Q_M combine to form Q_T following the same law as resistances in parallel.

If additionally, we choose r₁ at the optimum value described above where

then Q_M is simplified to

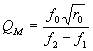
We have discussed already how Q_M and Q_A are different names for the same quantity.

Measurement “In Box”

If the driver is mounted already in a sealed box and is to be used that way, then the “In Air” measurement is all that is needed. The same applies generally to closed-back tweeters, whose “low frequency” parameters will be measured around their resonances in the region of 1 kHz to 2 kHz.

However in the more usual case, and in any case if we also want to know the driver’s sensitivity, we will need to know the additional parameter V_AS which expresses the compliance of a driver in terms of an equivalent volume of air. Other more elaborate measurements have been proposed, but the original method is simple and delivers the parameter directly in the form in which it is most useful.

Two methods are proposed in ref.1 for measuring V_AS.

The first, in its eqns (100) to (104) makes the measurement in a totally enclosed box, without a vent, and was preferred at the time of writing the paper. However, after experience using that method, it became clear that if the box was not completely sealed, through leakage at the joints or around the mounting hole for the driver, some quite anomalous results could be obtained. For those reasons the writer now prefers the second method using a vented box and outlined in eqns (105) to (108) of ref. 1. Although leaks are still undesirable in this method, they contribute only subsidiary, if somewhat resistive, vents that impair the measurements less. The tuning of the box is not critical, but should not be too far away from the resonance frequency f_S of the driver.

Testing in a Vented Box

With the driver mounted in the box, the impedance exhibits two peaks, as in Fig 9, at f_H and f:_L . Then f_B the resonance frequency of the box, is measured. In the original paper, this was taken as the frequency of minimum impedance, called f_B- in Fig. 9. However two difficulties arise when f_B is measured in this straightforward manner. The first is that the minimum of such a shallow trough is difficult to read.

The second is that the actual minimum read in this way is not the true f_B but rather the frequency where the voice coil inductance is in series resonance with the capacitive component of the motional impedance that is rising with decreasing frequency towards f_L.

This had produced little error in the initial work. At that time, voice coils were underhung, so as to ensure maximum efficiency when they were driven by valve amplifiers, and their inductance was comparatively small. However, with the advent of overhung voice coils the inductance increased and the error became significant. The problem was overcome by Benson [14], who took a further reading f_C at the frequency of the peak impedance when the vent is closed, as shown in the dashed curve which has been added in Fig 9, with other changes, to Fig. 5 of ref. 1. Then the true f_B is found from

It is worthwhile checking this figure against f_B-- , the frequency of the impedance minimum near f_B where the driver impedance Z_E goes through zero phase angle, which was taken as f_B in ref. 1. The true value for f_B should be the higher by a small amount.

Then the compliance V_AS , expressed as a volume of air, is found from

where V_B is the box volume. Also f_SB , the effective resonance frequency of the driver where it is mounted in the box, is found from

When a driver is mounted in a box the air mass loading on its cone doubles compared with its value unbaffled, so the resonance frequency f_SB falls, usually around 5% lower than f_SA , the resonance frequency previously measured in air with the driver unbaffled. This again is a useful check for consistency in the results, see eqns (105) and (106) in ref. 1. The effective Q’s with the driver mounted in the box, which we call Q_MB Q_EB and Q_TB, are also increased slightly from the earlier values, which we now call Q_MA Q_EA and Q_TA, to

At the same time, the leakage parameter Q_L is derived from the resistance R_B measured at f_B in Fig. 5, which is a little greater than R_E.

This is calculated as

This expression again is different from eqn (107) for Q_B in ref. 1, omitting the term (w_B/w_S )( C_AB/C_AS ). Initially Thiele had considered Q_B to be a parameter of the box, but Small found it to be primarily a property of the driver, a “leakage parameter” Q_L , which is independent of the box parameters, or the ratios of f_B to f_S or of V_B to V_AS. Note that when the expression for Q_L is derived directly from measurements of currents, it includes Q_TB . When the expression is derived from resistance measurements, or from the “r” ratios, it includes Q_M. Note that the ratio of compliances C_AS/C_AB is identical, in acoustic terms, to the ratio of air volumes V_AS/V_B .

Testing in an Enclosed Box.

In spite of the disadvantages described earlier of testing with a totally enclosed box, occasions arise when it may be unavoidable. A particular case is the measurement of V_AS in a closed-back tweeter.

The first set of readings is taken “in air” and f_SA Q_MA Q_EA and Q_TA calculated as before. Then the driver is placed in a box of volume V_B (in the case of the closed-back tweeter, the box, quite a small one, is placed in front of it) with suitable precautions that they seal tightly. Then a second set of similar readings are taken using the same procedures described earlier as “in air”, and parameters calculated which we will call f_SC Q_MC and Q_EC. From these we find

Then we find the ratio M_ASA/M_ASB of the masses of cone plus air load “in air” to “in box”

and use its square root as a multiplier to find f_SB Q_MB Q_EB and Q_TB

: : :

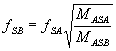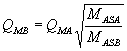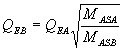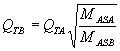
For the closed-back tweeter, which effectively has a baffle in both measurements, M_ASA/M_ASB should be unity, a useful check on the accuracy of the measurements.

Voice Coil Inductance L_E

Fig 10 (a) shows the voice coil inductance as it is usually represented, a pure inductance L in series with R_E the d.c. resistance and Z_M the motional impedance. However ref. 1 suggested a better model of driver impedance whose increase at the higher frequencies was limited by a resistance R₁ shunting the inductance L₁ in Fig 10 (b). This simplistic model may have been based on faulty observation, but it seemed to describe the drivers of the time, which had generally shorter, underhung, voice coils that had smaller inductances and in which the mechanisms described below were less significant.

Fifteen years later, Thiele used this model in developing a Zobel network to compensate the driver’s input impedance to produce a resistive termination for passive crossover networks [15], a shunt network containing R_E in series with a dual of the remainder of the driver impedance. However, Small found that model inadequate for the more recent drivers with longer voice coils, and produced a better fit to measured values using the model of Fig 10 (d), including its R₁ L₁ R₂ and L₂ but omitting R₃ and L₃ . Finally, Dash, a student of Small’s, developed an even better model [16] as in Fig 10 (c), a continuous structure comprising an infinite number of very large resistances and very small inductances. Adopted and published some years later by Vanderkooy [17], it is recognised today as the best available.

In this model the “pure” voice coil inductance is modified by eddy current losses in the pole piece to become a “semi-inductance”. This semi-inductance has the special quality that its reactance increases with Öw rather than w and that, at all frequencies, its impedance has series components of resistance and reactance that are equal, i.e. they present an impedance of the form R + jR that varies as the square root of frequency. Thus it can be written as KÖw + jKÖw and has a constant phase angle of 45°. When the resistance is written as KÖw, the inductance is K /Öw.

It will be seen from this model that a measurement of L_E at any frequency is valid at that frequency alone, and gives only a very rough approximation to the true, smaller, reactance at higher frequencies, and that there is an equal series resistance, both of them varying with Öf. Nevertheless, this figure for L_E , and even better the time constant T_E , provide a useful guide to the performance of a driver, from which its properties at other frequencies may be inferred.

We calculate L_E at f_ZMIN as 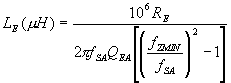and

Secondary Parameters.

Once the primary parameters have been found, as above, they may be combined into secondary parameters that convey further useful information about a driver.

Force Factors [18] provide figures of merit that split the efficiency (sensitivity) of a driver into two parts

F_ME, the magneto-electrical force factor, which depends purely on the motor, and

F_AM , the acousto-mechanical force factor, which depends purely on the area of the cone and its mass, including that of the voice coil.

The two factors are not used directly for the design of loudspeaker systems, but allow variations between different models of driver or inconsistencies in production to be evaluated precisely in the two separate aspects.

The magneto-electrical force factor is

__

F_ME = Bl /Ö R_E

where B is the flux density in the air-gap, l is the length of wire in the voice coil lying effectively within the air-gap and R_E is the resistance of the voice coil.

Rather than measuring B and establishing l, which is difficult particularly with an overhung voice coil, part of which lies in the fringing magnetic field, it can be estimated from the primary parameters

__________

F_ME = 149.4 S_D /Ö f_SB V_AS Q_EB

when all quantities are specified in SI units, i.e. the cone area S_D is in m², the driver resonance frequency f_SB in Hz, V_AS in m³ and F_ME in Newtons per Watts^1/2. It should be noted that the square of this parameter, namely

F²_ME = ( B l )² / R_E

is described as “thrust” by loudspeaker engineers in the U.K. The second, acousto-mechanical, force factor is ________

F_AM = Ö(r_o / 4 p c)( S_D/M_MS)

where M_MS is the mass of the cone in kilograms and F_AM is in units of Watts^1/2 per Newton. This factor also is most easily derived from the primary parameters as

F_AM = 4.671 f_SB²V_AS /10⁶ S_D

In more familiar units, when V_AS is in litres (dm³) and S_D (mm²) is expressed indirectly in terms of d_C the effective cone diameter in mm, then

__________

F_ME = 0.00371 d_C² / Ö f_SB V_AS Q_EB and F_AM = 0.00595 f_SB² V_AS / d_C²

Small has shown that S_D can usually be taken with little error as the area measured to the middle of the surround.

Power Available Efficiency (PAE).

By multiplying F_ME and F_AM together and squaring that product we find the Power Available Efficiency, PAE or h

h = ( F_ME F_AM )² = 8.0 f_SB³V_AS /10¹² Q_EB when V_AS is in in³

= 487 f_SB³V_AS /10¹² Q_EB when V_AS is in litres (dm³)

Efficiency is usually used in electrical engineering to describe the ratio of the energy or power going into a device to the energy or power that comes out of it, calculated as

Efficiency h = W_OUT / W_IN

Power is defined conventionally in terms of the voltage E applied to, or the current I flowing into, a resistance R, thus

W = E²/R = I² R

However, a driver presents an impedance to the external circuit whose resistive component varies widely with frequency, even while its output remains substantially constant. For this reason it is impractical to use the actual, varying, value of the driver impedance but to rate its efficiency in terms of PAE, where W_IN is not the power going into the driver but rather the power that would have gone into a pure resistance equal to the d.c. resistance R_E of the voice coil.

Sound Pressure Level.

Rather than by efficiency, the sensitivity of a driver is more often rated by the sound pressure level (SPL) that it produces at a distance of 1 metre in half-space from an electrical input power (available power as defined above) of 1 Watt. This is derived from the PAE value as follows.

An acoustic power of 1 acoustic Watt radiated non-directionally into 2p steradians half-space, i.e. full space divided into two by an infinite plane (e.g. a vertical wall) produces an acoustic pressure of

Ö r_oc /2p Pascal (N/m²) at 1 metre distance. When the ambient temperature T is 22° C and the barometric pressure is 10⁵ Pascal (751 mm Hg), then r_o the density of air is 1.188 kg/m³, c the velocity of sound is 344.5 m/s and the acoustic pressure thus generated is 8.060 Pascal. Expressed in dB relative to a reference sound pressure of 20 mPascal, which is taken as a standard pressure level at the threshold of human hearing, this is 112.1 dB SPL.

Once the Power Available Efficiency of a driver is found in decibels

dB PAE = 10 log₁₀PAE

which is a negative quantity since PAE is less than unity, then the driver can be rated as

dB SPL, 1W, 1m = 112.1 dB + dB PAE

Thus a driver with a PAE of 1% is rated as having either an efficiency h of -20.0 dB, or alternatively, an output SPL at 1 metre distance, with 1 Watt input, of +92.1 dB.

Further, the convention has arisen of specifying SPL in terms of an input voltage of 2.83 Volts rather than an input power of 1 Watt. A voltage of 2.83 Volts produces 1 Watt power in a resistance of 8 ohms, and such a specification obviates the need to establish the value of the voice coil resistance R_E . It also makes a driver with a low voice coil resistance rate as more sensitive because it draws more power from a transistor amplifier, which performs as a source of voltage. By this criterion then, which accords with practice when it is fed from an amplifier with a very low output impedance, a driver with a d.c. resistance of 4 ohms is 3.0 dB more sensitive than if its resistance had been 8 ohms with nothing else changed, and

dB SPL, 2.83 V, 1m = 112.1 dB + dB PAE + 10 log₁₀ (8/R_E)

Note that this expression includes R_E , which should not be confused with the rated impedance of the driver. That, conventionally, is higher than R_E , being usually taken at the frequency f_ZMIN , where the impedance is resistive but also includes, in series with R_E , resistive components from the motional impedance and the semi-inductance of the voice coil.

Conclusion.

The paper has sought to present, in as compact a form as possible, the loudspeaker parameters that allow the amplitude, phase and transient responses of a system to be presented using the same techniques as for an electrical high-pass filter. Then a loudspeaker’s performance can be estimated by well-established techniques of computation.

The parameters are estimated from measurements of the input impedance of the driver, again using well-established electrical techniques, with the only ‘acoustical’ device employed a testing box of known internal volume.

It has not been shown how the background theory was derived from the electrical equivalents of acoustical quantities, or how devices can be modified to achieve more favourable designs. The prime object has been to collect into the one place the techniques of measurement and calculation from the divers places where they were described and present them in a form best suited to their effective use.

Acknowledgement.

The author gratefully acknowledges the assistance of Graeme Huon in helpful discussions and in editing.

References.

1. A. N. Thiele - Loudspeakers in Vented Boxes -

Proc. IRE Australia, Vol. 22, No. 8, 1961 August, pp. 487–508

reprinted J Audio Eng Soc, Vol. 19, Nos. 5 & 6, 1971 May & June, pp. 382–392 & 471–483

2. Richard H. Small – Direct Radiator Loudspeaker System Analysis –

J Audio Eng Soc, Vol 20 No 5, 1972 June, pp. 383-395

3. Richard H. Small – Closed Box Loudspeaker Systems, Part I Small Signal Analysis – J Audio Eng Soc, Vol 20 No 5, 1972 December

4. Richard H. Small – Closed Box Loudspeaker Systems, Part II Large Signal Analysis – J Audio Eng Soc, Vol 21 No 1, 1973 January/February

5. Richard H. Small – Vented Box Loudspeaker Systems, Part I Small Signal Analysis – J Audio Eng Soc, Vol 21 No 2, 1973 March

6. Richard H. Small – Vented Box Loudspeaker Systems, Part II Large Signal Analysis – J Audio Eng Soc, Vol 21 No 6, 1973 July/August

7. Richard H. Small – Vented Box Loudspeaker Systems, Part III Synthesis – J Audio Eng Soc, Vol 21 No 6, 1973 July/August

8. Richard H. Small – Vented Box Loudspeaker Systems, Part IV Appendices – J Audio Eng Soc, Vol 21 No 7, 1973 September

9. L. L. Beranek – Acoustics – McGraw-Hill, London, 1954 reprinted American Institute of Physics, New York, 1986, Figs 5.3 & 5.9, pp.119 & 127

10. Wolfgang Klippel – Dynamic Measurements and Interpretation of the Nonlinear Parameters of Electrodynamic Loudspeakers – J Audio Eng Soc, Vol 38 No 10, 1990 December, pp.944-955

11. A. N. Thiele - Loudspeakers, Enclosures and Equalisers -

Proc. IREE Australia, Vol. 34, No. 11, November 1973, pp. 425–448

12. Neville Thiele - An Active Biquadratic Filter for Equalizing Overdamped Loudspeakers –

AES 116^th Convention, Berlin, Germany, 2004 May 8-11, Preprint No. 6153, 14 pp.

13. Neville Thiele - Phase Considerations in Loudspeaker Systems -

AES 110^th Convention, Amsterdam, The Netherlands, 12-15 May 2001, Preprint No. 5307, 13pp.

14. J. E. Benson – Theory and Design of Loudspeaker Enclosures Part 3 – Introduction to Synthesis of

Vented Systems – AWA Technical Review, Vol 14 No 4, 1974, Appendix 4, eqn A4-6, p.471

reprinted as Theory and Design of Loudspeaker Enclosures –

Synergetic Audio Concepts, Don & Carolyn Davis, 1993, 244 pp.

15. A. N. Thiele - Optimum Passive Loudspeaker Dividing Networks -

Proc. IREE Australia, Vol. 36, No. 7, July 1975, pp. 220–224

16. I. M. Dash – An Equivalent Circuit Model for the Moving Coil Loudspeaker –

honours thesis 1982, School of Electrical Engineering, University of Sydney, Australia

17. John Vanderkooy - A Model of Loudspeaker Driver Impedance including Eddy Currents in the Pole

Structure – J Audio Eng Soc, Vol. 37, No. 3, March 1989, pp. 119-128

18. A. N. Thiele - Force Conversion Factors of a Loudspeaker Driver – JEEEA,Vol. 13, No.2, June 1993, pp.129-131 & reprinted J Audio Eng Soc, Vol. 41, No. 9, September 1993, pp. 701-703

Note: References nos. 1-8 reprinted in “Loudspeakers, An Anthology, Vol.1 – Vol.25 (1953-1977)”,

ed. R.E.Cooke, Audio Engineering Society, New York, 1978

References nos. 10 & 16 reprinted in “Loudspeakers, An Anthology, Volume 4, Transducers,

Measurement and Evaluation, Vol.32 – Vol.39 (1984-1991)”,

ed. Mark R Gander, Audio Engineering Society, New York, 1996

References 1, 5-8 & 11 reprinted IREE, Australia in “Vented Loudspeakers – An Anthology”.

-oOo-

Figures.

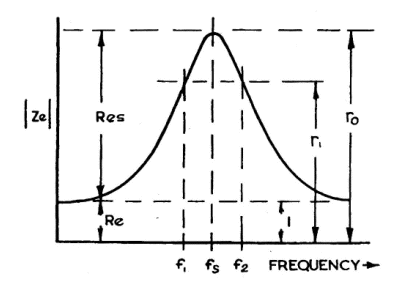
Figure 1 - Simplified electrical equivalent circuit of the loudspeaker

Figure 2 - Typical impedance curve of loudspeaker (Modulus of Ze in figure 1)

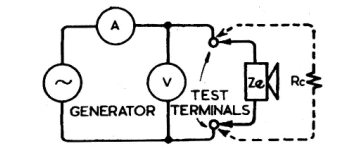
Figure 3 - Test circuit schematic for measurement of loudspeaker parameters

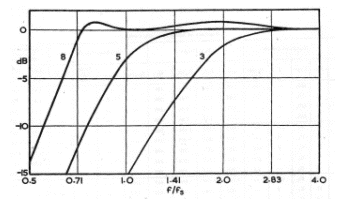
Curve No.	f3/fS	fB/fS	CAS/CAB	QT
3	1.77	1.42	4.46	0.26
5	1.00	1.00	1.42	0.38
8	0.64	0.76	0.56	0.52

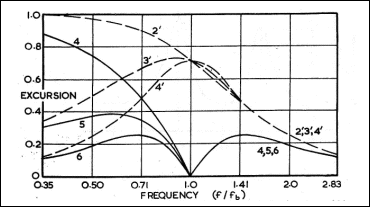
Figure 4 - Typical curves for a vented loudspeaker. Driver with the same resonance frequency fs, but different alignments comprising box resonance f_B, box size C_AS/C_AB and total Q_T

Figure 5 - Curves of cone excursion

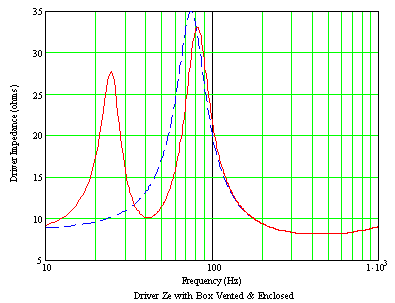
Figure 6a - Driver impedance in vented and enclosed box

Re = 8.0 ohms: Qe = 0.50: Qm = 2.00: Ql = 7 .00: Fs = 50.0 Hz: Fb = 40.0 Hz: Vas/Vb = 1.20: Le = 800 uH

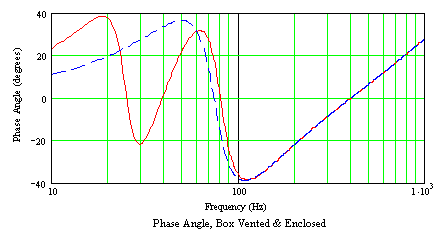
Figure 6b - Driver phase angle of driving impedance for vented and enclosed box

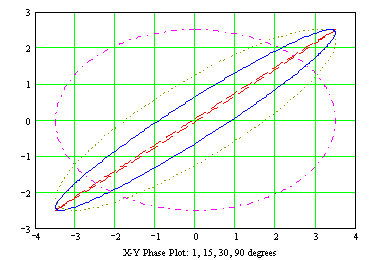
Dashed curve - 1 deg: Solid curve - 15 deg: Dotted curve - 30 deg: Dash-dot curve - 90 deg

Figure 7 - Oscilloscope X-Y phase plot

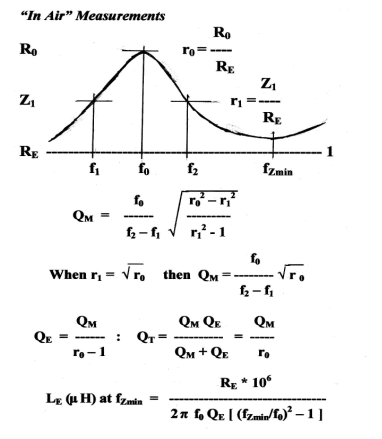
Figure 8 - Driver measurements “In air”

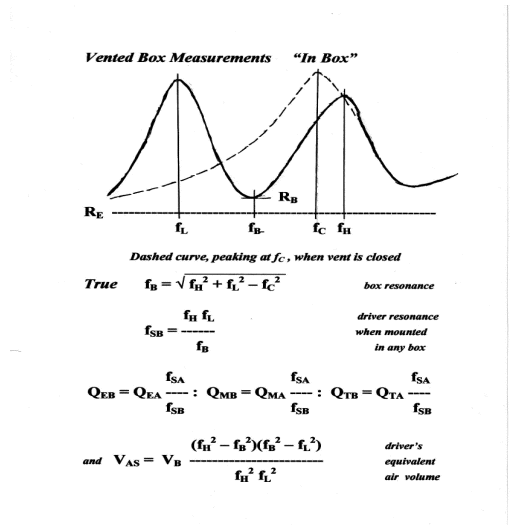
Figure 9 - Vented box measurements “in box”

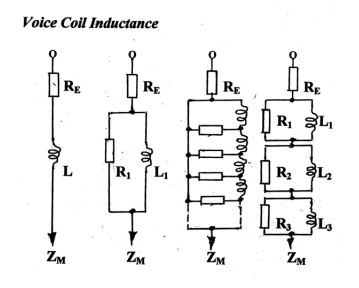
(a) (b) (c) (d)

Figure 10 - Simplified electrical equivalent circuits of the loudspeaker voice coil.

Z_M is the motional impedance modelled by L_ces C_mes and R_es in Fig 1.